Ömer
Yönetici
geometrik şekiller ve özellikleri nelerdir
Bu yazımızda detaylı şekilde Geometrik şekiller hakkında bilgiler vereceğiz sizlere
Üçgen
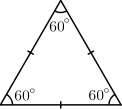
Bir üçgen, düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir.
Düzlem geometrisinin temel şekillerinden biridir. Bir üçgenin üç köşesi ve bu köşeleri birleştiren, doğru parçalarından oluşan üç kenarı vardır. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.
Üçgenin iç açıları toplamı 180 derecedir.
Bir ABC üçgenine, A tepe noktasından teğet geçecek ve BC ye paralel olacak şekilde bir doğru çizildiğinde, BC doğru parçasının açıları, iç ters açılar kuralından dolayı tepe açısının yanına gelerek bir doğru parçasının yarısını kaplarlar.
Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
Bir ABD üçgenine, D tepe noktasından teğet geçecek ve taban olan BC ye paralel olacak şekilde bir doğru çizilip kenarlar uzatıldığında, yöndeş açılar kuralı yardımıyla bu önerme kanıtlanabilir.
Üçgenler, kendilerini oluşturan parçaların (köşe, kenar, açılar vb.) aynı düzlemde olup olmadığına göre sınıflandırılabilir. Eğer üçgenin tamamı tek bir düzlemdeyse düzlemsel, diğer durumlarda da örneğin küresel ya da hiperbolik üçgen terimleri kullanılır.
Eşkenar üçgen
Tüm kenarları eşit olan üçgendir. Tüm iç açıları 60°'dir. Tabanlara indirilen dikmeler hem açıortay, hem de kenarortaydır.
İkizkenar üçgen
İki kenarı eşit olan üçgenlerdir. Ayrıca iki açısı birbirine eşitir. Eşit olmayan kenara indirilen dikme hem açıortay hem kenarortay özelliği gösterir.
Çeşitkenar üçgen
Her kenarının uzunluğu farklı olan üçgenlerdir. Tüm iç açıları birbirinden farklıdır. Çeşitkenar üçgenin simetri ekseni yoktur.
Dar Açılı Üçgen
Açıları 90 dereceden küçük olan üçgenlere denir.
Dik Açılı Üçgen
Bir açısı dik (90°) olan üçgenlerdir. Bu üçgenlerde yükseklik dik kenarlardan biridir. En uzun kenarına hipotenüs denir.
Geniş Açılı Üçgen
Açılarından biri 90°den geniş olan üçgenlerdir. Sadece bir tek açısı geniş açı olabilir. Tabana ait yükseklik tabanın uzantısı ile kesişir.
Bu yazımızda detaylı şekilde Geometrik şekiller hakkında bilgiler vereceğiz sizlere
Üçgen

Bir üçgen, düzlemde birbirine doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimidir.
Düzlem geometrisinin temel şekillerinden biridir. Bir üçgenin üç köşesi ve bu köşeleri birleştiren, doğru parçalarından oluşan üç kenarı vardır. Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir.
Üçgenin iç açıları toplamı 180 derecedir.
Bir ABC üçgenine, A tepe noktasından teğet geçecek ve BC ye paralel olacak şekilde bir doğru çizildiğinde, BC doğru parçasının açıları, iç ters açılar kuralından dolayı tepe açısının yanına gelerek bir doğru parçasının yarısını kaplarlar.
Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
Bir ABD üçgenine, D tepe noktasından teğet geçecek ve taban olan BC ye paralel olacak şekilde bir doğru çizilip kenarlar uzatıldığında, yöndeş açılar kuralı yardımıyla bu önerme kanıtlanabilir.
Üçgenler, kendilerini oluşturan parçaların (köşe, kenar, açılar vb.) aynı düzlemde olup olmadığına göre sınıflandırılabilir. Eğer üçgenin tamamı tek bir düzlemdeyse düzlemsel, diğer durumlarda da örneğin küresel ya da hiperbolik üçgen terimleri kullanılır.
Eşkenar üçgen
Tüm kenarları eşit olan üçgendir. Tüm iç açıları 60°'dir. Tabanlara indirilen dikmeler hem açıortay, hem de kenarortaydır.
İkizkenar üçgen
İki kenarı eşit olan üçgenlerdir. Ayrıca iki açısı birbirine eşitir. Eşit olmayan kenara indirilen dikme hem açıortay hem kenarortay özelliği gösterir.
Çeşitkenar üçgen
Her kenarının uzunluğu farklı olan üçgenlerdir. Tüm iç açıları birbirinden farklıdır. Çeşitkenar üçgenin simetri ekseni yoktur.
Dar Açılı Üçgen
Açıları 90 dereceden küçük olan üçgenlere denir.
Dik Açılı Üçgen
Bir açısı dik (90°) olan üçgenlerdir. Bu üçgenlerde yükseklik dik kenarlardan biridir. En uzun kenarına hipotenüs denir.
Geniş Açılı Üçgen
Açılarından biri 90°den geniş olan üçgenlerdir. Sadece bir tek açısı geniş açı olabilir. Tabana ait yükseklik tabanın uzantısı ile kesişir.
Son düzenleme: