Ömer
Yönetici
DİK PRİZMALARIN ALAN ve HACİMLERİ
Alt ve üst tabanları paralel eş şekillerden oluşan cisimlere prizma denir. Yan yüzeyleri taban düzlemine dik olan prizmalara dik prizma adı verilir.
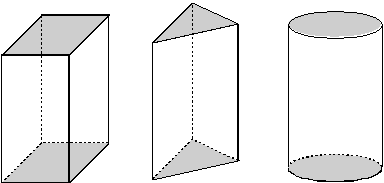
Prizmalarda yan yüzeyleri birleştiren ayrıtlara yanal ayrıt denir.
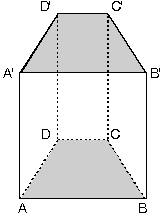
[AA'], [BB'], [CC'], [DD'] yanal ayrıtlardır.
Dik prizmalarda yanal ayrıt cismin yüksekliğine eşittir.
Cismin yüksekliğine h dersek
h = |AA'| = |BB'| = |CC'| = |DD'| olur.
Prizmanın Hacmi
Hacim = Taban Alanı x Yükseklik
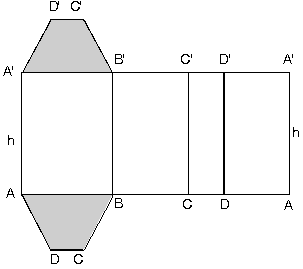
Dik prizmanın taban biçimi nasıl olursa olsun, yanal yüzeyi daima bir dikdörtgen olur. Yanal yüzü oluşturan dikdörtgenin alt kenarı tabanın çevresi kadardır. Diğer kenarı ise h yüksekliği kadar olur.
Yanal Alan = Taban çevresi x Yükseklik
Bütün dik prizmaların yanal alanı taban çevresi ile yüksekliğin çarpımıdır. Bütün Alan ise yanal alan ile iki taban alanının toplamıdır.
Tüm Alan = Yanal Alan + 2. Taban Alanı
1. Dikdörtgenler Prizması
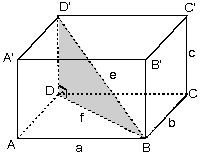
Dikdörtgenler prizması yan yüzeyleri karşılıklı ikişer ikişer eş olan altı adet dikdörtgenden oluşan prizmadır. Burada hacim, taban alanı olan (a.b) ile yükseklik olan (c) nin çarpımıdır. Alan ise (a.b), (b.c) ve (a.c) yüzey alanlarının ikişer katlarının toplamıdır. Dikdörtgenler prizmasında birbirine en uzak iki köşeyi birleştiren doğru parçasına cisim köşegeni denir.
Cisim köşegeni daima prizmanın içinden geçer. Yüzeylerinden geçmez. Sadece bir yüzeyden geçen köşegene o yüze ait yüzey köşegeni denir. Burada köşegenlerin uzunlukları:
|AC'| = |A'C| = |BD'| = |B'D| = e (cisim köşegeni)
|BD| = f (Yüzey köşegeni) olsun. Bu durumda
Hacim = a.b.c
Alan =2(ab+bc+ac)
Alan = 2 (ab + bc + ac)
Cisim Köşegeni: e =
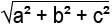
Yüzey Köşegeni: f =
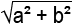
2. Kare Prizma
Tabanı kare olan prizmalara kare prizma denir. Yan yüzü dört adet eş dikdörtgenden oluşur.

Hacim = a² . h
Yanal Alan = 4 . a . h
Alan = 4.ah + 2.a²
Cisim köşegeni : e =
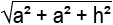
3. Küp
Bütün ayrıtları birbirine eşit olan dik prizmaya küp denir. Tüm yüzeyleri kare dir.

Hacim = a³
Alan = 6a²
Kübün yüzey köşegenleri birbirine eşittir.
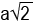
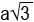
4. Üçgen Prizmalar
Prizmalar tabanlarının şekline göre isim aldıklarından tabanı üçgen olan prizmalara üçgen prizma denir.
Üçgen prizmalar tabanını oluşturan üçgene göre isimlenir.
a. Eşkenar Üçgen Prizma
Eşkenar üçgen prizmanın tabanları eşkenar üçgendir. Yan yüzeyleri ise üç tane eş dikdörtgenden oluşur.Tabanı eşkenar üçgen olduğundan

Tabanı eşkenar üçgen olduğundan
Taban alanı
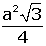 Hacim
Hacim

Taban çevresi 3a olduğundan, yanal alan 3a.h dır.
Buradan tüm alanı
Tüm alan
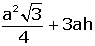
b. Dik Üçgen Prizma
Dik üçgen prizmanın tabanı dik üçgendir. Yan yüzeyleri ise üç tane dikdörtgenden oluşur.

Tabanı dik üçgen olduğundan
Taban alanı =
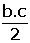 Hacim
Hacim
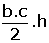
Taban çevresi a + b + c olduğundan,
Yanal alan = (a + b + c) . h
Tüm Alan = b . c + (a + b + c) . h
5. Silindir
Tabanı daire olan prizmalara silindir denir. Silindirin yan yüzü dikdörtgen biçimindedir. Dikdörtgenin bir kenarı yükseklik kadar, diğer kenarı ise taban dairesinin çevresi kadardır.

Taban alanı= πr²
Hacim= πr²h
Taban çevresi πr olduğundan yanal alan 2πrh olur.
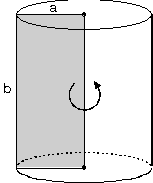
Tüm alan = 2πrh+ 2πr Bir dikdörtgen levha bir kenarı etrafında döndürüldüğünde silindir elde edilir.
6. Düzgün Çokgen Prizmalar
Tabanı düzgün çokgenlerden oluşan prizmalara düzgün çokgen prizmalar deriz. Taban ayrıtları birbirine eşittir. Diğer dik prizmalarda olduğu gibi düzgün çokgen prizmalarda da yanal ayrıt aynı zamanda yüksekliktir.
Dik prizmalarda taban şekli ne olursa olsun, hacmin taban alanı ile yüksekliğin çarpımı ve yanal alanın ise taban çevresi ile yüksekliğin çarpımı olduğunu unutmayalım.
EĞİK PRİZMALAR
1. Eğik Kare Prizma

Tabanı, bir kenarı a olan kareden oluşan prizma bir yöne doğru taban düzlemi ile a açısı yapacak kadar eğilirse eğik kare prizma elde edilir.
Prizmanın yanal ayrıtlarına l dersek,
Prizmanın yüksekliği h =l .sin α olur.
Eğik prizmanın yanal ayrıtlarına dik olacak şekilde oluşan kesitine dik kesit denir. Eğik kare prizmanın iki yan yüzeyi dikdörtgen, diğer iki yan yüzeyi ise paralelkenardır.
Eğik kare prizmanın dik kesitinin bir kenarı taban kenarı a kadar, diğeri ise,
a'=a.sin α kadardır.
Buradan;
Dik Kesit Alanı = Taban Alanı x Sin α
Dik kesit çevresi = 2a +2a.sin α
Eğik prizmaların yanal alanlarının toplamı
Yanal alan= Dik kesit çevresi x Yanal Ayrıt
bağıntısı ile bulunur. Alt ve üst tabanlar ilave edildiğinde tüm alan bulunmuş olur. Bütün prizmalarda olduğu gibi eğik prizmalarda da hacim, taban alanı ile yüksekliğin çarpımı ile bulunur.
Hacim = Taban Alanı x Yükseklik
Ayrıca dik kesit alanı ile yanal ayrıtın çarpımı ile de hacim bulunabilir.
Hacim = Dik Kesit Alanı x Yanal Ayrıt
2. Eğik Silindir

|AA'| = |BB'| = l
Yanal ayrıtı l olan ve taban düzlemi ile a açısı yapan eğik silindirde yükseklik,
h=l.sin α
Dik Kesit Alanı=Taban Alanı x Sin a
Eğik silindirin yan yüz alanı, dik kesit çevresi ile yanal ayrıtının çarpımıdır. Bütün eğik prizmalarda olduğu gibi eğik silindir de de hacim, dik kesit alanı ile yanal ayrıtın çarpımına eşittir.
Hacim = Taban Alanı x Yükseklik
Hacim = Dik Kesit Alanı x Yanal Ayrıt
Yanal Alan = Dik Kesit Çevresi x Yanal Ayrıt
Alt ve üst tabanları paralel eş şekillerden oluşan cisimlere prizma denir. Yan yüzeyleri taban düzlemine dik olan prizmalara dik prizma adı verilir.

Prizmalarda yan yüzeyleri birleştiren ayrıtlara yanal ayrıt denir.

[AA'], [BB'], [CC'], [DD'] yanal ayrıtlardır.
Dik prizmalarda yanal ayrıt cismin yüksekliğine eşittir.
Cismin yüksekliğine h dersek
h = |AA'| = |BB'| = |CC'| = |DD'| olur.
Prizmanın Hacmi
Hacim = Taban Alanı x Yükseklik

Dik prizmanın taban biçimi nasıl olursa olsun, yanal yüzeyi daima bir dikdörtgen olur. Yanal yüzü oluşturan dikdörtgenin alt kenarı tabanın çevresi kadardır. Diğer kenarı ise h yüksekliği kadar olur.
Yanal Alan = Taban çevresi x Yükseklik
Bütün dik prizmaların yanal alanı taban çevresi ile yüksekliğin çarpımıdır. Bütün Alan ise yanal alan ile iki taban alanının toplamıdır.
Tüm Alan = Yanal Alan + 2. Taban Alanı
1. Dikdörtgenler Prizması

Dikdörtgenler prizması yan yüzeyleri karşılıklı ikişer ikişer eş olan altı adet dikdörtgenden oluşan prizmadır. Burada hacim, taban alanı olan (a.b) ile yükseklik olan (c) nin çarpımıdır. Alan ise (a.b), (b.c) ve (a.c) yüzey alanlarının ikişer katlarının toplamıdır. Dikdörtgenler prizmasında birbirine en uzak iki köşeyi birleştiren doğru parçasına cisim köşegeni denir.
Cisim köşegeni daima prizmanın içinden geçer. Yüzeylerinden geçmez. Sadece bir yüzeyden geçen köşegene o yüze ait yüzey köşegeni denir. Burada köşegenlerin uzunlukları:
|AC'| = |A'C| = |BD'| = |B'D| = e (cisim köşegeni)
|BD| = f (Yüzey köşegeni) olsun. Bu durumda
Hacim = a.b.c
Alan =2(ab+bc+ac)
Alan = 2 (ab + bc + ac)
Cisim Köşegeni: e =
Yüzey Köşegeni: f =
2. Kare Prizma
Tabanı kare olan prizmalara kare prizma denir. Yan yüzü dört adet eş dikdörtgenden oluşur.

Hacim = a² . h
Yanal Alan = 4 . a . h
Alan = 4.ah + 2.a²
Cisim köşegeni : e =
3. Küp
Bütün ayrıtları birbirine eşit olan dik prizmaya küp denir. Tüm yüzeyleri kare dir.

Hacim = a³
Alan = 6a²
Kübün yüzey köşegenleri birbirine eşittir.
4. Üçgen Prizmalar
Prizmalar tabanlarının şekline göre isim aldıklarından tabanı üçgen olan prizmalara üçgen prizma denir.
Üçgen prizmalar tabanını oluşturan üçgene göre isimlenir.
a. Eşkenar Üçgen Prizma
Eşkenar üçgen prizmanın tabanları eşkenar üçgendir. Yan yüzeyleri ise üç tane eş dikdörtgenden oluşur.Tabanı eşkenar üçgen olduğundan

Tabanı eşkenar üçgen olduğundan
Taban alanı
Taban çevresi 3a olduğundan, yanal alan 3a.h dır.
Buradan tüm alanı
Tüm alan
b. Dik Üçgen Prizma
Dik üçgen prizmanın tabanı dik üçgendir. Yan yüzeyleri ise üç tane dikdörtgenden oluşur.

Tabanı dik üçgen olduğundan
Taban alanı =
Taban çevresi a + b + c olduğundan,
Yanal alan = (a + b + c) . h
Tüm Alan = b . c + (a + b + c) . h
5. Silindir
Tabanı daire olan prizmalara silindir denir. Silindirin yan yüzü dikdörtgen biçimindedir. Dikdörtgenin bir kenarı yükseklik kadar, diğer kenarı ise taban dairesinin çevresi kadardır.

Taban alanı= πr²
Hacim= πr²h
Taban çevresi πr olduğundan yanal alan 2πrh olur.

Tüm alan = 2πrh+ 2πr Bir dikdörtgen levha bir kenarı etrafında döndürüldüğünde silindir elde edilir.
6. Düzgün Çokgen Prizmalar
Tabanı düzgün çokgenlerden oluşan prizmalara düzgün çokgen prizmalar deriz. Taban ayrıtları birbirine eşittir. Diğer dik prizmalarda olduğu gibi düzgün çokgen prizmalarda da yanal ayrıt aynı zamanda yüksekliktir.
Dik prizmalarda taban şekli ne olursa olsun, hacmin taban alanı ile yüksekliğin çarpımı ve yanal alanın ise taban çevresi ile yüksekliğin çarpımı olduğunu unutmayalım.
EĞİK PRİZMALAR
1. Eğik Kare Prizma

Tabanı, bir kenarı a olan kareden oluşan prizma bir yöne doğru taban düzlemi ile a açısı yapacak kadar eğilirse eğik kare prizma elde edilir.
Prizmanın yanal ayrıtlarına l dersek,
Prizmanın yüksekliği h =l .sin α olur.
Eğik prizmanın yanal ayrıtlarına dik olacak şekilde oluşan kesitine dik kesit denir. Eğik kare prizmanın iki yan yüzeyi dikdörtgen, diğer iki yan yüzeyi ise paralelkenardır.
Eğik kare prizmanın dik kesitinin bir kenarı taban kenarı a kadar, diğeri ise,
a'=a.sin α kadardır.
Buradan;
Dik Kesit Alanı = Taban Alanı x Sin α
Dik kesit çevresi = 2a +2a.sin α
Eğik prizmaların yanal alanlarının toplamı
Yanal alan= Dik kesit çevresi x Yanal Ayrıt
bağıntısı ile bulunur. Alt ve üst tabanlar ilave edildiğinde tüm alan bulunmuş olur. Bütün prizmalarda olduğu gibi eğik prizmalarda da hacim, taban alanı ile yüksekliğin çarpımı ile bulunur.
Hacim = Taban Alanı x Yükseklik
Ayrıca dik kesit alanı ile yanal ayrıtın çarpımı ile de hacim bulunabilir.
Hacim = Dik Kesit Alanı x Yanal Ayrıt
2. Eğik Silindir

|AA'| = |BB'| = l
Yanal ayrıtı l olan ve taban düzlemi ile a açısı yapan eğik silindirde yükseklik,
h=l.sin α
Dik Kesit Alanı=Taban Alanı x Sin a
Eğik silindirin yan yüz alanı, dik kesit çevresi ile yanal ayrıtının çarpımıdır. Bütün eğik prizmalarda olduğu gibi eğik silindir de de hacim, dik kesit alanı ile yanal ayrıtın çarpımına eşittir.
Hacim = Taban Alanı x Yükseklik
Hacim = Dik Kesit Alanı x Yanal Ayrıt
Yanal Alan = Dik Kesit Çevresi x Yanal Ayrıt
Son düzenleme: