cicozz
Çocukluk cicozlarda saklı
Akor Hakkında Bilgiler
Akor Nedir ?
AKOR:
Üç veya daha fazla sesin aynı anda tınlamasına akor denir.
Her çalgı ile akor çalınamaz. Akor çalabilen çalgıların başında piyano ve
gitar gelir. Bu çalgılarda aynı anda üç ve üçden fazla ses çalınabilir.
Bu nedenle gerek piyano ve gerekse gitar çok iyi birer solo çalgı
oldukları gibi çok da iyi birer eşlik çalgısıdırlar.
Gitardaki akor kalıplarına geçmeden önce notaların simgelerini öğrenelim.
Notaların karşılığı olan harf simgeleri şöyledir:
La= A
Si= B
Do= C
Re= D
Mi= E
Fa= F
Sol= G
Bundan sonraki bölümde gitar üzerinde akor basmayı öğreneceğiz...
Bilindiği gibi Batı Müziğinde iki ana akor vardır. MAJÖR ve MİNÖR.
Tek başına bir "C" gördüğümüz zaman bu "Do Majör" akoru demektir.
Eğer "C"nin yanında küçük "m" harfi varsa "Cm" bu da "Do minör"
demektir.Bu bütün akorlar için geçerlidir.
Şimdi en sık kullanılan akorları resimleriyle beraber görelim:
La Minör Akoru Am
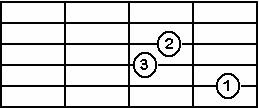
Mi Major Akoru E
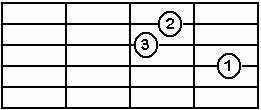
Re Minör Akoru Dm
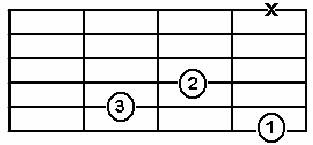
Do majör akoru C
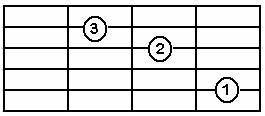
Re Major Akoru D
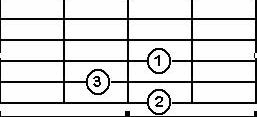
Sol Major Akoru G
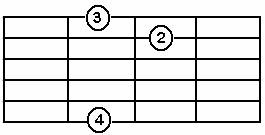
Si Major Yedili Akoru B7
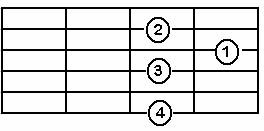
La Major Akoru A
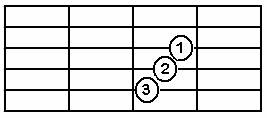
Mi Minör Akoru Em
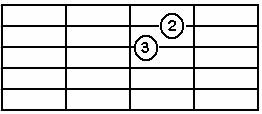
Fa Major Akoru (Bare) F
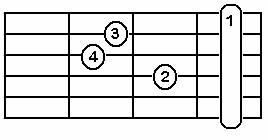
Yukarıda bulunun akorlar Temel akorlardır fakat bunların yanında yüzlerce akor daha bulunmakta, aynı zamanda her akorun da birden fazla basma şekli var... Bu yüzden kategoriler halinde diger akorlar gosterilebilir... Önce bu tekniği nasıl okuyacağınız anlatayım... vereceğim akorlar için bir örnek vermek istiyorum yukarda resimli olarak verilen akorlardan birini seçerek...
Örneğin La Major (A) akoru bu teknikte şu şeklide yazılmaktadır:
A----- 0 0 2 2 2 0
Şimdi açıklamaya gelirsek, burada yanyana altı adet rakam bulunmakta... Rakamların sırası gitarın en üst telinden en alt teline doğrudur... Yani en soldaki 0 en üstteki telini (Kalın Mi teli), en sağdaki 0 da en alttaki telini (İnce Mi teli) ifade eder... Tele karşılık gelen sıradaki rakam ise o tel üzerinde kaçıncı perdeye basacağınız gösterir... Bu bilgilere göre okuyacak olursak:
0 ---- En üstteki telde herhangi bir perde basılı olmayacak
0 ---- İkinci telde herhangi bir perde basılı olmayacak
2 ---- Üçüncü telde ikinci perdeye basılacak
2 ---- Dördüncü telde ikinci perdeye basılacak
2 ---- Beşinci telde ikinci perdeye basılacak
0 ---- En alttaki telde herhangi bir tele basılmayacak...
Bu açıklama ile resimdeki akoru karşılaştırmanız daha kolay anlamanızı sağlayacaktır...

Bu akor yazılış tekniğinde henagi bir sırada "x" işareti görürseniz, bu o tele akor vurulurken dokunulmayacağı anlamına gelmektedir... Yani akoru çalarken o telden ses çıkarmamak için o tele dokunmayacaksınız... Şİmdi kategoriler halinde akorlarımızı bu yeni teknikte görelim....
Akor Nedir ?
AKOR:
Üç veya daha fazla sesin aynı anda tınlamasına akor denir.
Her çalgı ile akor çalınamaz. Akor çalabilen çalgıların başında piyano ve
gitar gelir. Bu çalgılarda aynı anda üç ve üçden fazla ses çalınabilir.
Bu nedenle gerek piyano ve gerekse gitar çok iyi birer solo çalgı
oldukları gibi çok da iyi birer eşlik çalgısıdırlar.
Gitardaki akor kalıplarına geçmeden önce notaların simgelerini öğrenelim.
Notaların karşılığı olan harf simgeleri şöyledir:
La= A
Si= B
Do= C
Re= D
Mi= E
Fa= F
Sol= G
Bundan sonraki bölümde gitar üzerinde akor basmayı öğreneceğiz...
Bilindiği gibi Batı Müziğinde iki ana akor vardır. MAJÖR ve MİNÖR.
Tek başına bir "C" gördüğümüz zaman bu "Do Majör" akoru demektir.
Eğer "C"nin yanında küçük "m" harfi varsa "Cm" bu da "Do minör"
demektir.Bu bütün akorlar için geçerlidir.
Şimdi en sık kullanılan akorları resimleriyle beraber görelim:
La Minör Akoru Am

Mi Major Akoru E

Re Minör Akoru Dm

Do majör akoru C

Re Major Akoru D

Sol Major Akoru G

Si Major Yedili Akoru B7

La Major Akoru A

Mi Minör Akoru Em

Fa Major Akoru (Bare) F

Yukarıda bulunun akorlar Temel akorlardır fakat bunların yanında yüzlerce akor daha bulunmakta, aynı zamanda her akorun da birden fazla basma şekli var... Bu yüzden kategoriler halinde diger akorlar gosterilebilir... Önce bu tekniği nasıl okuyacağınız anlatayım... vereceğim akorlar için bir örnek vermek istiyorum yukarda resimli olarak verilen akorlardan birini seçerek...
Örneğin La Major (A) akoru bu teknikte şu şeklide yazılmaktadır:
A----- 0 0 2 2 2 0
Şimdi açıklamaya gelirsek, burada yanyana altı adet rakam bulunmakta... Rakamların sırası gitarın en üst telinden en alt teline doğrudur... Yani en soldaki 0 en üstteki telini (Kalın Mi teli), en sağdaki 0 da en alttaki telini (İnce Mi teli) ifade eder... Tele karşılık gelen sıradaki rakam ise o tel üzerinde kaçıncı perdeye basacağınız gösterir... Bu bilgilere göre okuyacak olursak:
0 ---- En üstteki telde herhangi bir perde basılı olmayacak
0 ---- İkinci telde herhangi bir perde basılı olmayacak
2 ---- Üçüncü telde ikinci perdeye basılacak
2 ---- Dördüncü telde ikinci perdeye basılacak
2 ---- Beşinci telde ikinci perdeye basılacak
0 ---- En alttaki telde herhangi bir tele basılmayacak...
Bu açıklama ile resimdeki akoru karşılaştırmanız daha kolay anlamanızı sağlayacaktır...

Bu akor yazılış tekniğinde henagi bir sırada "x" işareti görürseniz, bu o tele akor vurulurken dokunulmayacağı anlamına gelmektedir... Yani akoru çalarken o telden ses çıkarmamak için o tele dokunmayacaksınız... Şİmdi kategoriler halinde akorlarımızı bu yeni teknikte görelim....