Ömer
Yönetici
PERMÜTASYON
A. SAYMANIN TEMEL KURALI
1) Ayrık iki işlemden biri m yolla, diğeri n yolla yapılabiliyorsa, bu işlemlerden biri veya diğeri m + n yolla yapılabilir.
2) İki işlemden birincisi m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m . n yolla yapılabilir.
1. Toplama Kuralı
Sonlu ve ayrık kümelerin eleman sayılarının toplamı, bu kümelerin birleşimlerinin elemanlarının sayısına eşittir. Sonlu ve ayrık iki küme A ve B olsun
s(A) = m
s(B) = n
s(A ᴖ B ) = ø
olmak üzere,
s(A ᴗ B ) = s(A) + s(B)
= m + n dir.
Sonuç
Ayrık iki işlemden biri m yolla diğeri n yolla yapılabiliyorsa, bu işlemlerden biri veya diğeri m + n yolla yapılabilir.
2. Çarpma Kuralı
2 tane elemandan oluşan (a1, a2) ifadesine sıralı ikili denir. Benzer biçimde
(a1, a2, a3) ifadesine sıralı üçlü
(a1, a2, a3, a4) ifadesine sıralı dörtlü
. . .
(a1, a2, a3, ... , an) ifadesine sıralı n li denir.
A ve B sonlu iki küme olsun
s(A) = m
s(B) = n
olmak üzere,
s(A . B) = s(A) . s(B) = m . n dir.
A . B kümesi birinci bileşenleri A dan ikinci bileşenleri B den alınan sıralı ikililerden oluşur.
Sonuç
İki işlemden birincisi m yolla yapılabiliyorsa ve ilk işlem bu m yoldan birisiyle yapıldıktan sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte
m . n
yolla yapılabilir.
B. FAKTÖRİYEL
1 den n ye kadar olan sayma sayılarının çarpımına n faktöriyel denir ve n! biçiminde gösterilir.
0! = 1
1! = 1
2! = 1.2 = 2
3! = 1.2.3 = 6
4! = 1.2.3.4 = 24
Sonuç
n! = n . (n - 1)!
= n . (n - 1) . (n - 2)!
C. PERMÜTASYON (SIRALAMA) TANIMI
r ve n sayma sayısı ve r £ n olmak üzere, n elemanlı bir kümenin r elemanlı sıralı r lilerine bu kümenin r li permütasyonları denir.
n elemanlı kümenin r li permütasyonlarının sayısı,
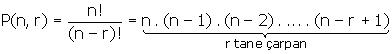
Sonuç
1. P(n, n) = n!
2. P(n, 1) = n
3. P(n, n – 1) = n! dir.
D. TEKRARLI PERMÜTASYON
n tane nesnenin; n1 tanesi 1. çeşitten, n2 tanesi 2. çeşitten, ... , nr tanesi de r yinci çeşitten olsun.
n = n1 + n2 + n3 + ... + nr
olmak üzere, bu n tane nesnenin n li permütasyonlarının sayısı,
E. DAİRESEL (DÖNEL) PERMÜTASYON
n tane farklı elemanın dönel (dairesel) sıralanmasına, n elemanın dairesel sıralaması denir.
n elemanın dairesel sıralamalarının sayısı :
(n – 1)! dir.
n tane farklı anahtarın yuvarlak (halka biçimindeki) bir anahtarlığa sıralanmalarının
sayısı :
KOMBİNASYON
TANIM
r ve n birer doğal sayı ve r ∈ n olmak üzere, n elemanlı bir A kümesinin r elemanlı alt kümelerinin her birine, A kümesinin r li kombinasyonu (gruplaması) denir.
n elemanın r li kombinasyonlarının sayısı
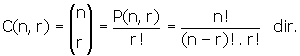
Permütasyonda sıralama, kombinasyonda ise seçme söz konusudur.
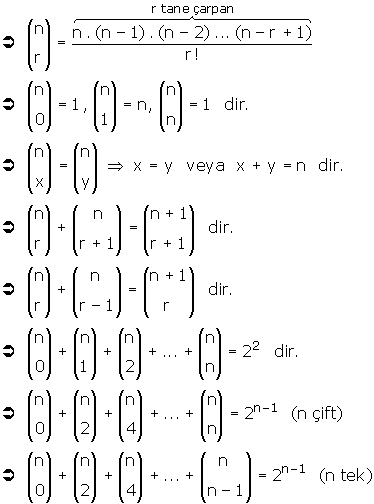
• n kenarlı düzgün bir çokgenin köşegen sayısı:
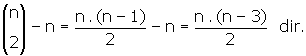
• Herhangi üçü doğrusal olmayan, aynı düzlemde bulunan n tane noktayla;
a) Çizilebilecek doğru sayısı
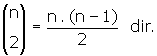
b) Köşeleri bu noktalar üzerinde olan
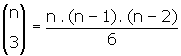
• Aynı düzlemde birbirine paralel olmayan n tane doğru en çok
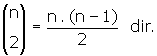
noktada kesişirler.
• Aynı düzlemde bulunan doğrulardan n tanesi birbirine paralel ve bu n tane doğruya paralel olmayan diğer m tane doğru da birbirine paraleldir.
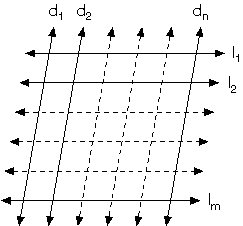
Düzlemde kenarları bu doğrular üzerinde olan
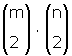
• Aynı düzlemde yarıçapları farklı n tane çemberin en çok
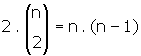
noktası vardır.
BİNOM AÇILIMI
A. TANIM
n doğal sayı olmak üzere,
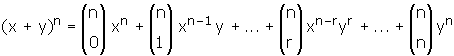
ifadesine binom açılımı denir.
Burada;
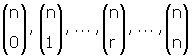
sayılarına binomun kat sayıları denir.
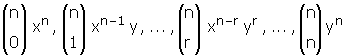
ifadelerinin her birine terim denir.
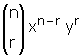
B. (x + y)n AÇILIMININ ÖZELİKLERİ
1) (x + y)n açılımında (n + 1) tane terim vardır.
2) Her terimdeki x ve y çarpanlarının üslerinin toplamı n dir.
3) Kat sayılar toplamını bulmak için değişkenler yerine 1 yazılır. Buna göre, (x + y)n nin katsayılarının toplamı (1 + 1)n = 2n dir.
4) (x + y)n ifadesinin açılımı x in azalan kuvvetlerine göre dizildiğinde;
baştan (r + 1). terim :
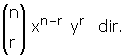
sondan (r + 1). terim :
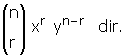
(x – y)n ifadesinin açılımında 1. terimin işareti (+), 2. terimin işareti (–), 3. terimin işareti (+) ... dır.
Kısaca; y nin üssü çift sayı olan terimin işareti (+), tek sayı olan terimin işareti (–) dir.
• n pozitif doğal sayı olmak üzere,
(x + y)2n nin açılımında ortanca terim
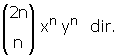
• n pozitif doğal sayı olmak üzere,
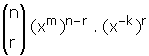
ifadesinde m . (n – r) – kr = 0 koşulunu sağlayan n ve r değerleri yazılarak bulunur.
• c bir gerçel sayı olmak üzere, (x + y + c)n açılımındaki sabit terimi bulmak için x = 0 ve y = 0 yazılır.
• (a + b + c)n nin açılımında ak . br . cm li terimin kat sayısı;
Son düzenleme: