Ömer
Yönetici
İKİNCİ ve ÜÇÜNCÜ DERECEDEN DENKLEMLER
A. TANIM
a, b, c gerçel sayı ve a ¹ 0 olmak üzere,
ax2 + bx + c = 0
biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir.
Bu açık önermeyi doğrulayan x sayılarına denklemin kökleri; tüm köklerin oluşturduğu kümeye denklemin çözüm kümesi; çözüm kümesini bulmak için yapılan işlemlere denklem çözme; a, b, c sayılarına da denklemin kat sayıları denir.
B. İKİNCİ DERECEDEN DENKLEMİN ÇÖZÜM KÜMESİNİN BULUNUŞU
1. Çarpanlara Ayırma Yöntemi
ax2 + bx + c = 0 denklemi f(x) . g(x) = 0
biçiminde yazılabiliyorsa
f(x) = 0 veya g(x) = 0 olup çözüm kümesi;
Ç = {x | x, f(x) = 0 veya Q(x) = 0 denklemini sağlar} olur.
2. Diskiriminant (D) Yöntemi
ax2 + bx + c = 0 denklemi a ¹ 0 ve D = b2 – 4ac ise, çözüm kümesi
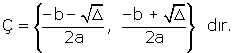
ax2 + bx + c = 0
denkleminde, D = b2 – 4ac olsun.
a) D > 0 ise, denklemin farklı iki gerçel kökü vardır.
Bu kökleri,
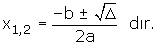
b) D < 0 ise, denklemin gerçel kökü yoktur.
c) D = 0 ise, denklemin eşit iki gerçel kökü vardır.
Bu kökler,
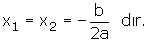
Denklemin bu köklerine; eşit iki kök, çakışık kök ya da çift katlı kök denir.
Ü ax2 + bx + c = 0
denkleminin kökleri simetrik ise,
1) b = 0 ve a ¹ 0 dır.
2) Simetrik kökleri gerçel ise,
b = 0, a ¹ 0 ve a . c £ 0 dır.
C. İKİNCİ DERECEDEN DENKLEMİN KÖKLERİ İLE KAT SAYILARI ARASINDAKİ
BAĞINTILAR
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 ise,
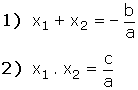
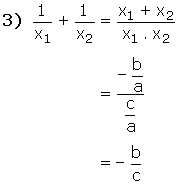
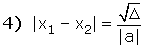
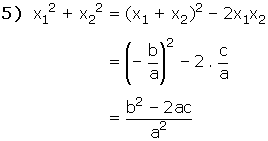
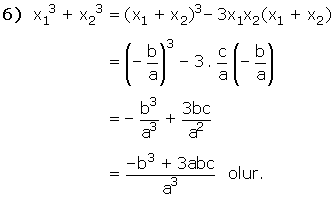
D. KÖKLERİ VERİLEN İKİNCİ DERECEDEN DENKLEMİN YAZILMASI
Kökleri x1 ve x2 olan ikinci dereceden denklem;
(x – x1) (x – x2) = 0 dır. Bu ifade düzenlenirse,
x2 – (x1 + x2)x + x1x2 = 0 olur.
Ü ax2 + bx + c = 0 ... (1) denkleminin kökleri x1 ve x2 olsun.
Kökleri mx1 + n ve mx2 + n olan ikinci dereceden denklem, (1) denkleminde x yerine
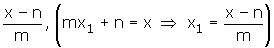yazılarak bulunur.
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0 denklemlerinin çözüm kümeleri aynı ise,
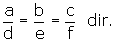
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0
denklemlerinin sadece birer kökleri eşit ise,
ax2 + bx + c = dx2 + ex + f
(a – d)x2 + (b – e)x + c – f = 0 dır.
Bu denklemin kökü verilen iki denklemi de sağlar.
ÜÇÜNCÜ DERECEDEN DENKLEMLER
A. TANIM
a ¹ 0 olmak üzere, ax3 + bx2 + cx + d = 0 biçimindeki denklemlere üçüncü dereceden bir bilinmeyenli denklemler denir.
B. ÜÇÜNCÜ DERECEDEN DENKLEMİN KÖKLERİ İLE KAT SAYILARI ARASINDAKİ
BAĞINTILAR
a ¹ 0 ve ax3 + bx2 + cx + d = 0 denkleminin kökleri x1, x2 ve x3 olsun. Buna göre,
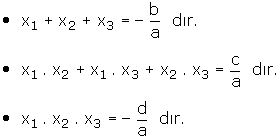
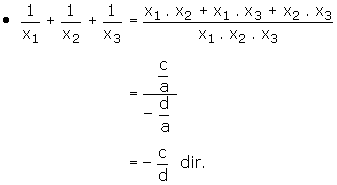
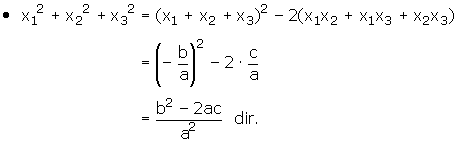
C. KÖKLERİ VERİLEN ÜÇÜNCÜ DERECE DENKLEMİN YAZILMASI
Kökleri x1, x2 ve x3 olan üçüncü derece denklem
(x – x1) (x – x2) (x – x3) = 0 dır.
Bu denklem düzenlenirse,
x3 – (x1 + x2 + x3)x2 + (x1x2 + x1x3 + x2x3)x – x1x2x3 = 0 olur.
Ü ax3 + bx2 + cx + d = 0 denkleminin kökleri x1, x2, x3 olsun.
1) Bu kökler aritmetik dizi oluşturuyorsa,
x1 + x3 = 2x2 dir.
2) Bu kökler geometrik dizi oluşturuyorsa,
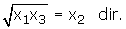
3) Bu kökler hem aritmetik hem de geometrik dizi oluşturuyorsa,
x1 = x2 = x3 tür.
Ü n, 1 den büyük pozitif tam sayı olmak üzere,
anxn + an – 1xn – 1 + ... + a1x + a0 = 0
denkleminin;
Kökleri toplamı :
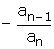
Kökleri çarpımı :
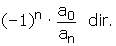
A. TANIM
a, b, c gerçel sayı ve a ¹ 0 olmak üzere,
ax2 + bx + c = 0
biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir.
Bu açık önermeyi doğrulayan x sayılarına denklemin kökleri; tüm köklerin oluşturduğu kümeye denklemin çözüm kümesi; çözüm kümesini bulmak için yapılan işlemlere denklem çözme; a, b, c sayılarına da denklemin kat sayıları denir.
B. İKİNCİ DERECEDEN DENKLEMİN ÇÖZÜM KÜMESİNİN BULUNUŞU
1. Çarpanlara Ayırma Yöntemi
ax2 + bx + c = 0 denklemi f(x) . g(x) = 0
biçiminde yazılabiliyorsa
f(x) = 0 veya g(x) = 0 olup çözüm kümesi;
Ç = {x | x, f(x) = 0 veya Q(x) = 0 denklemini sağlar} olur.
2. Diskiriminant (D) Yöntemi
ax2 + bx + c = 0 denklemi a ¹ 0 ve D = b2 – 4ac ise, çözüm kümesi
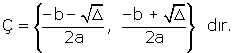
ax2 + bx + c = 0
denkleminde, D = b2 – 4ac olsun.
a) D > 0 ise, denklemin farklı iki gerçel kökü vardır.
Bu kökleri,
b) D < 0 ise, denklemin gerçel kökü yoktur.
c) D = 0 ise, denklemin eşit iki gerçel kökü vardır.
Bu kökler,
Denklemin bu köklerine; eşit iki kök, çakışık kök ya da çift katlı kök denir.
Ü ax2 + bx + c = 0
denkleminin kökleri simetrik ise,
1) b = 0 ve a ¹ 0 dır.
2) Simetrik kökleri gerçel ise,
b = 0, a ¹ 0 ve a . c £ 0 dır.
C. İKİNCİ DERECEDEN DENKLEMİN KÖKLERİ İLE KAT SAYILARI ARASINDAKİ
BAĞINTILAR
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 ise,
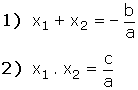
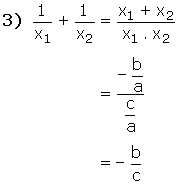
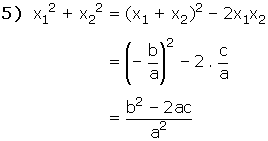
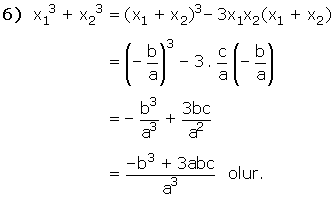
D. KÖKLERİ VERİLEN İKİNCİ DERECEDEN DENKLEMİN YAZILMASI
Kökleri x1 ve x2 olan ikinci dereceden denklem;
(x – x1) (x – x2) = 0 dır. Bu ifade düzenlenirse,
x2 – (x1 + x2)x + x1x2 = 0 olur.
Ü ax2 + bx + c = 0 ... (1) denkleminin kökleri x1 ve x2 olsun.
Kökleri mx1 + n ve mx2 + n olan ikinci dereceden denklem, (1) denkleminde x yerine
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0 denklemlerinin çözüm kümeleri aynı ise,
Ü ax2 + bx + c = 0 ve dx2 + ex + f = 0
denklemlerinin sadece birer kökleri eşit ise,
ax2 + bx + c = dx2 + ex + f
(a – d)x2 + (b – e)x + c – f = 0 dır.
Bu denklemin kökü verilen iki denklemi de sağlar.
ÜÇÜNCÜ DERECEDEN DENKLEMLER
A. TANIM
a ¹ 0 olmak üzere, ax3 + bx2 + cx + d = 0 biçimindeki denklemlere üçüncü dereceden bir bilinmeyenli denklemler denir.
B. ÜÇÜNCÜ DERECEDEN DENKLEMİN KÖKLERİ İLE KAT SAYILARI ARASINDAKİ
BAĞINTILAR
a ¹ 0 ve ax3 + bx2 + cx + d = 0 denkleminin kökleri x1, x2 ve x3 olsun. Buna göre,
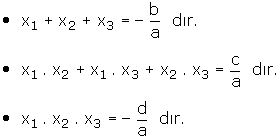
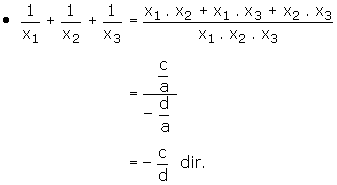
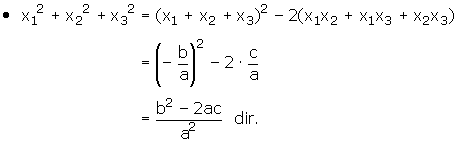
C. KÖKLERİ VERİLEN ÜÇÜNCÜ DERECE DENKLEMİN YAZILMASI
Kökleri x1, x2 ve x3 olan üçüncü derece denklem
(x – x1) (x – x2) (x – x3) = 0 dır.
Bu denklem düzenlenirse,
x3 – (x1 + x2 + x3)x2 + (x1x2 + x1x3 + x2x3)x – x1x2x3 = 0 olur.
Ü ax3 + bx2 + cx + d = 0 denkleminin kökleri x1, x2, x3 olsun.
1) Bu kökler aritmetik dizi oluşturuyorsa,
x1 + x3 = 2x2 dir.
2) Bu kökler geometrik dizi oluşturuyorsa,
3) Bu kökler hem aritmetik hem de geometrik dizi oluşturuyorsa,
x1 = x2 = x3 tür.
Ü n, 1 den büyük pozitif tam sayı olmak üzere,
anxn + an – 1xn – 1 + ... + a1x + a0 = 0
denkleminin;
Kökleri toplamı :
Kökleri çarpımı :
Son düzenleme:
