Ömer
Yönetici
A. HARFLİ İFADELER
4a, 2(x – y), x2, a + b + 3c gibi ifadelere harfli ifadeler denir.
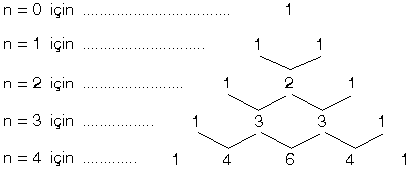
(a + b)n açılımı yapılırken, önce a nın n . kuvvetten başlayarak azalan, b nin 0 dan başlayarak artan kuvvetlerinin çarpımları yazılıp toplanır. Sonra n nin Paskal üçgenindeki karşılığı bulunarak katsayılar belirlenir. (a – b)n yukarıdaki biçimde yapılır ancak b nin; çift kuvvetlerinde terimin önüne (+), tek kuvvetlerinde terimin önüne (–) işareti konulur.
Örnek
C. ÖZDEŞLİKLER
Çözüm kümesi R (Reel Sayılar) olan eşitliklere özdeşlik denir.
1. İki Kare Farkı - Toplamı
D. ORTAK ÇARPAN PARANTEZİNE ALMA
Her terimde kat sayıların e.b.o.b. u veya her terimdeki aynı (ortak) çarpan ifadelerin parantez dışına alınmasına denir.
E. GRUPLANDIRMA
Verilen ifadenin terimleri uygun şekillerde gruplara ayrılır ve ayrılan gruplarda ortak bir çarpan aranır.
F. x2 + bx + c
BİÇİMİNDEKİ ÜÇ TERİMLİNİN ÇARPANLARA AYRILMASI
b = m + n ve c = m . n olmak üzere, x2 + bx + c = (x + m) (x + n) dir.
4a, 2(x – y), x2, a + b + 3c gibi ifadelere harfli ifadeler denir.
- 3x2y ifadesinde 3 e kat sayı denir.
- Harfli ifadelerde, eksi (–) veya artı (+) işaretleriyle birbirinden ayrılan kısımlara terim denir.
- Harfleri ve harflerin kuvvetleri aynı olan terimlere de benzer terimler denir.

(a + b)n açılımı yapılırken, önce a nın n . kuvvetten başlayarak azalan, b nin 0 dan başlayarak artan kuvvetlerinin çarpımları yazılıp toplanır. Sonra n nin Paskal üçgenindeki karşılığı bulunarak katsayılar belirlenir. (a – b)n yukarıdaki biçimde yapılır ancak b nin; çift kuvvetlerinde terimin önüne (+), tek kuvvetlerinde terimin önüne (–) işareti konulur.
Örnek
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a – b)3 = a3 – 3a2b + 3ab2 – b3
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
- (x ± y)n açılımının her teriminindeki x ve y nin üsleri toplamı n dir.
- (x ± y)n açılımının terim sayısı n + 1 dir.
- (x ± y)n açılımında kat sayılar toplamını bulmak için x = y = 1 alınır.
C. ÖZDEŞLİKLER
Çözüm kümesi R (Reel Sayılar) olan eşitliklere özdeşlik denir.
1. İki Kare Farkı - Toplamı
- a2 – b2 = (a – b) (a + b)
- a2 + b2 = (a + b)2 – 2ab ya da
- a2 + b2 = (a – b)2 + 2ab dir.
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + ac + bc)
- (a + b – c)2 = a2 + b2 + c2 + 2(ab – ac – bc)
- a3 – b3 = (a – b) (a2 + ab + b2 )
- a3 + b3 = (a + b) (a2 – ab + b2 )
- a3 – b3 = (a – b)3 + 3ab (a – b)
- a3 + b3 = (a + b)3 – 3ab (a + b)
- (a – b)2n = (b – a)2n
- (a – b)2n – 1 = – (b – a)2n – 1 dir.
D. ORTAK ÇARPAN PARANTEZİNE ALMA
Her terimde kat sayıların e.b.o.b. u veya her terimdeki aynı (ortak) çarpan ifadelerin parantez dışına alınmasına denir.
E. GRUPLANDIRMA
Verilen ifadenin terimleri uygun şekillerde gruplara ayrılır ve ayrılan gruplarda ortak bir çarpan aranır.
F. x2 + bx + c
BİÇİMİNDEKİ ÜÇ TERİMLİNİN ÇARPANLARA AYRILMASI
b = m + n ve c = m . n olmak üzere, x2 + bx + c = (x + m) (x + n) dir.
Son düzenleme: